


Modeling
concentration fluctuations
What's it all about?
When modeling pollutant transport
and dispersion using gridded meteorological flow fields on an hourly basis,
significant parts of the turbulence spectra are not resolved in space and
time. Parameterizations of puff or plume dispersion commonly account for
this by estimating one-hour averaged dispersion (so-called "absolute dispersion").
For risk assessments and odor impact analyses, the highest possibly occurring
concentration during a time considerably shorter than one hour is more
decisive than one-hour average values. For this, the probability density
function of concentration for a given location and a specific averaging
time is required.
Use of the PPM to predict
concentration fluctuations
A method to estimate the higher
moments of near-source concentrations for different averaging times is
presented. Puff dispersion models using so-called "absolute dispersion"
predict one-hour-averaged concentrations. In order to be able to predict
the higher moments of concentration (the probability density function),
the "absolute dispersion" has to be separated in its puff-growth part and
the additional contribution from the meandering of the plume during the
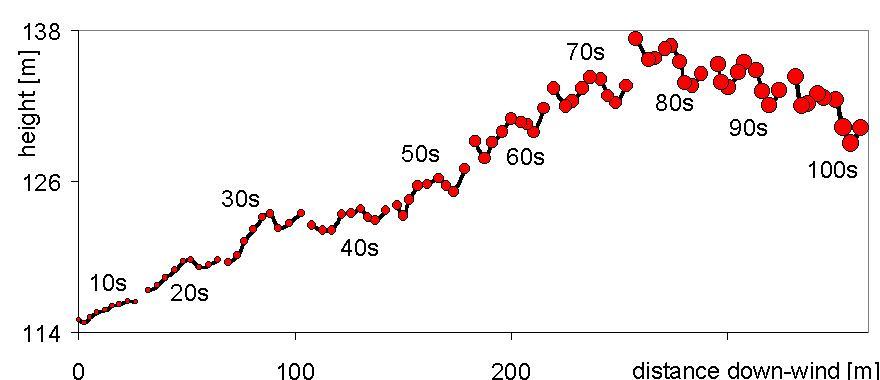
averaging time. The Puff-Particle Model (PPM) has been developed as such
a puff-meandering model. The PPM aims at combining the advantages of both,
puff and particle dispersion models by moving the center of mass of each
puff along a trajectory which mimics the quickly changing turbulent flow
field (artificial meandering). This trajectory is derived from the low-frequency
part of trajectories as simulated by a Lagrangian stochastic particle model.
These puff center trajectories are stochastically independent, which allows
only for the evaluation of instantaneous concentration variances. A puff-plume
meandering scheme is proposed which introduces spatial correlation between
puffs which simulate a continuously emitting source. With this approach,
the PPM can also be used to compute the probability density function for
any other given averaging time.
Further information...
...can be found in Chapter
5 of my PhD.
Or send me an e-mail: peter@dehaan.ch
Back to: Peter
de Haan's home page. last update: 4 Oct 2000 - PdH